CS 194-26 Project 2

Project 2 - Fun with Filters and Frequencies - CS 194-26

Eric Tang

Part 1 - Fun with Filters

Part 1.1 Finite Difference Operator

In this part, we used the finite difference filters of Dx = [1 -1] and Dy = [1 -1]^T in order to compute the magnitude of the gradient in the horizontal and vertical directions respectively, giving us gradient_x, and gradient_y.

Gradient Magnitude Computation

We then computed the overall gradient via the formula gradient = sqrt(gradient_x^2 + gradient_y^2).

Results

The images below are the partial derivative wrt x, the partial derivative wrt y, the gradient of the image, and the binarized gradient of the image (in that order).

Part 1.2 Derivative of Gaussian (DoG) Filter

In this section, we used the gaussian filter to blur our original image, then took the finite difference operators over the blurred image. We then formed DoG filters by convolving the finite difference operators with the gaussian, then convolving those filters with our images.

What differences do you see?

This approach yielded much clearer edges than we saw in part 1.1, since we avoided having to threshold out some amount of noise by blurring the image before taking the partial derivatives.

Verify that you get the same result as before with DoG filters

Results with the DoG filters were the same as those we got by separately blurring the images, and then taking the partial derivatives of the blurred images.

Results

Filters

These are the DoG filters for x and y (in that order).

Edges

These are the results of convolving the DoG filters with the original cameraman image. The images are in the following order: partial derivative wrt x, partial derivative wrt y, gradient magnitude, binarized gradient magnitude.

Part 2 - Fun with Frequencies

Part 2.1 - Image “Sharpening”

Naive Sharpening

We can sharpen images by amplifying the high frequency components of the images. We do this by taking a gaussian filter over the image to blur it, then subtracing the resulting low frequency features from the original image to get the high frequency features. We can then scale and add these high frequency features to the original image to get a sharpened version of it. The results of this approach are below. The original image is displayed first, followed by the image sharpened with alpha = [1, 2, 5] in that order.

Unsharp Mask Filter

We can combine the operations from the naive sharpening approach into a single convolution operation called the unsharp mask filter. Given an image f, a scaling factor alpha, the unit impulse e, and a gaussian filter, the unsharp mask filter is given by ((1 + alpha)*e - alpha*g). Convolving this with our image f gives us the sharpened version of our image, as in the previous section. Below are results for blurring a sharp image, and resharpening it using the unsharp mask filter. The original image is displayed first, followed by the blurred image, followed by the image resharpened using the unsharp mask filter.

Part 2.2 - Hybrid Images

We can create “Hybrid” images by taking the low frequency features of one image, and combining it with the high frequency features of another, and aligning them on top of another to create an image that looks different at different distances (the brain views low and high frequency features differently depending on distance of the image from the eyes). Below are some results of hybrid images.

Derek and Nutmeg

Hug and Efros (with Frequency Analysis)

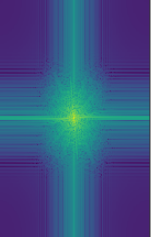
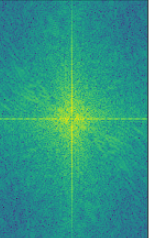
Carol Christ and Oski

Frown and Smile (Me)

Failure Case (Hug + Hilfinger)

This one looked pretty weird because their heads were different sizes in the images, and somehow looks like neither of them.

Part 2.3 - Gaussian and Laplacian Stacks

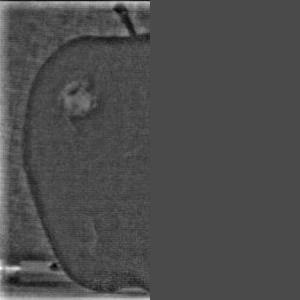
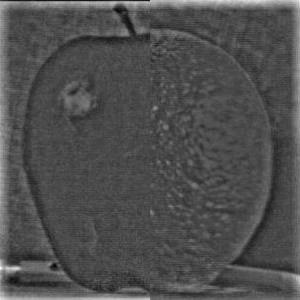
Part 2.4 Multiresolution Blending

Oraple

Irregular Mask (Me + Obama)

Shanghai Then vs Now

Coolest + Most Interesting + Most Important thing I learned

I thought that the multiresolution blending using the laplacian stacks was really cool - I really liked the output of blending shanghai then vs now, and playing around with the mask to get a nice looking output. The use of frequencies for hybrid images was also really interesting, and very important in understanding how we percieve different levels of features in images differently. I also learned that it’s pretty hard to align images and get them to be the same size for transferring their features to other images.